【终极一战】代数tv vs CG3.7, 你们知道吗

3.7! 终于可以给第三章收尾了

第一个 Thm 3.7.1 说的就是, 对于我们熟悉的 efh setting, 对任意 nilp. 总可以让他 fit 到某个 $e$ 里. 这就是所谓的 Jacobson-Morozov Thm.

Prop 3.7.3: 对上述的 $(e,f,h)$ is determined uniquely up to conj. by an element in $Z_G(e)$.

然后, 由于中间的都比较耳熟能详, 跳到 3.7.6:

Prop 3.7.6: Any nilp. orbit $\mathbb{O}\subset\mathfrak{g}^\ast$ is a $\mathbb{C}^\ast$-stable subvar.

Furthermore it is a symplectic cone-var. w.r.t. the canonical symplectic structure on a coadjoint orbit and the vector field $\xi=Eu$.

由于 $diag(t,t^{-1})$ 在 $e$ 上的作用是 $t^2e$, 我们给出 $\mathbb{O}\subset\mathfrak{g}^\ast$ $\mathbb{C}^\ast$-stable. 我们有, $\lambda\in \mathbb{O}$ 处的 symplectic 2-form is given by $w_{\lambda}(ad_x\lambda,ad_y\lambda)=\lambda([x,y])$. 而, 乘以 $c\in\mathbb{C}^\ast$ 保持 $\mathbb{O}$ 不变, 记这个映射诱导的切空间上映射为 $c_\ast$, 不难验证

对 $c=1$ 求导, 我们得到 $L_{Eu}w=w$, 即证.

后面那些关于 highest weight (也许, 他有些地方用的是 lowest weight, 他诗人握持) 的论断同样可以跳过.

Thm 3.7.13: Let $e_i$ set of root vectors that corres. to simple roots, then $x=\sum e_i$ is regular.

现在我们更几何地来看, 考虑 standard slices.

对于 $e$ nilp. $(e,f,h)$ $\mathfrak{sl}_2$-triple. 考虑 $\mathbb{O}$ 为 $e$ 对应的 $G$-conj class. $\mathfrak{s}=Z_{\mathfrak{g}}(f)$. 于是

Prop 3.7.15: The affine space $e+\mathfrak{s}$ is transverse to $\mathbb{O}$ in $\mathfrak{g}$. Moreover, we have $\mathbb{O}\cap (e+\mathfrak{s})=e$.

这 transverse 大概就是, $\ker f\oplus \operatorname{im} e=\mathfrak{g}$. 而后面那个?

在 $e+\mathfrak{s}$ 上定义 $\mathbb{C}^\ast$ 作用: $(t,e+s)\mapsto e+t^2(\operatorname{Ad}\gamma(t^{-1})s)$.

不难验证这确实是一个 $\mathbb{C}^\ast$ 作用. 而, 由于 $\mathfrak{s}$ 上的元素在这个作用下都拥有 strictly positive integer, 有

但, $\mathbb{O}$ 在如上定义的作用下 stable. 因此, 若 $\mathbb{O}\cap (e+\mathfrak{s})\backslash{e}$ 非空, 他在 $e$ 附近任意去心邻域内也应当非空. 但这就和 $\mathfrak{s}$ 与 $\mathbb{O}$ transverse 矛盾. 有点意思.

这松岛辉空打的跟一投注一样, 张本美和也有福了[捂脸]

但, 该说不说, 松岛这场打的还挺好的

虽然还是大突破口

Cor 3.7.19: The fibre $\mu^{-1}(e)\subset \tilde{\N}$ is a homotopy retract of $\tilde{S}=\mu^{-1}(e+\mathfrak{s})\subset \tilde{\N}$.

仍旧, 考虑 $e+\mathfrak{s}$ 上定义 $\mathbb{C}^\ast$ 作用: $(t,e+s)\mapsto e+t^2(\operatorname{Ad}\gamma(t^{-1})s)$. 由于 $\N$ stable under $\mathbb{C}^\ast$ 与 $Ad(G)$, 这个作用保持 $S=\N\cap e+\mathfrak{s}$ 不变. 同样的, 由于 $\mu:\tilde{\N}\to\N$ $G$-equiv, $\tilde{S}=\mu^{-1}(e+\mathfrak{s})$ 不变.

注意 $(e,\mathfrak{b})$ 在 $Ad(g)$ 的作用下的像是 $(Ad_ge,Ad_g\mathfrak{b})$, 即使在 $g$ 的作用下 $e$ 不变, 但 $Ad_g\mathfrak{b}$ 是会变得. 因此这并不能直接定义 retract. 我们要小小地 modify 一下:

在 $\tilde{S}$ 上定义vector field $v$ given by 这个 $\mathbb{C}^\ast$-action, 然后考虑 $r$ 是 $e+\mathfrak{s}$ 上的一个Euclidiean distance (其实, 为了是 $C^\infty$, 这里应该选取其平方). 然后, 把他 lift 到 $\tilde{S}$. 现在, 考虑 $-v\cdot \tilde{r}$, 其上的 flow 就给出了一个到 $\mu^{-1}(e)$ 的 retract.

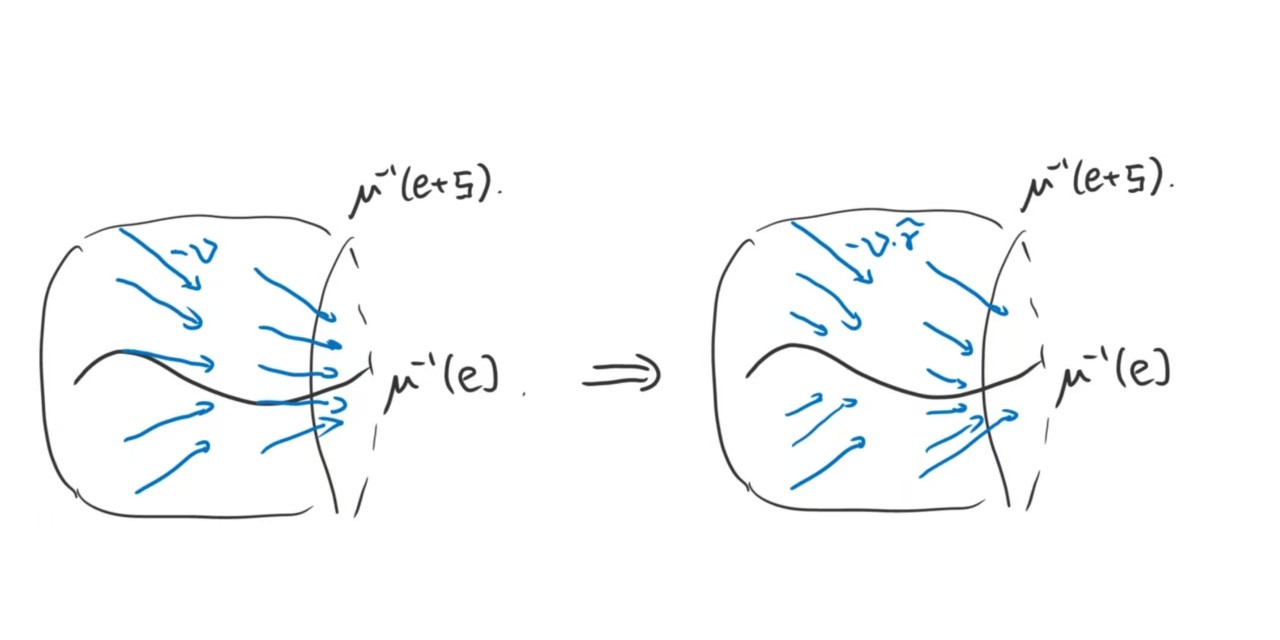
现在要研究 $Z_G(e)$, 有 $\operatorname{Lie}Z_G(e)=Z_\mathfrak{g}(e)$. by $(e,f,h)$ 的 setting 我们可以给出 $\mathfrak{g}$ 的 grading. 有 $\mathfrak{g}=\oplus \mathfrak{g}_i$, 取 $Z_i=\mathfrak{g}_i\cap Z_\mathfrak{g}(e)$, 那么有

考虑 $u=\oplus_{i>0}Z_i$, $U\subset Z_G(e)$ corre. unipotent normal subgp, 有

Lemma 3.7.21: (i) $\mathfrak{u}=\ker(e)\cap \operatorname{im} (e)$.

(ii) $h+\mathfrak{u}$ is stable under the adjoint $U$-action. Moreover, $h+\mathfrak{u}=U\cdot h$ is a single orbit.

(i) 是 triv 的. (ii) 由于 $[\mathfrak{u},\mathfrak{u}]\subset \mathfrak{u},[h,\mathfrak{u}]\subset \mathfrak{u}$, $U$ 的作用的 orbit open dense, 但由于 $U$ 幂零, orbit 又是closed. 因此是 $h+\mathfrak{u}$ 全体.

剩下的工作就是着手证明 3.7.3 和 3.7.1 了. 大概 sketch 一下:

1. $(e,f,h)$ 和 $(e,f^\prime,h^\prime)$ two $\mathfrak{sl}_2$ triple, then $h^\prime=h\implies f^\prime=f$. 这是因为 $f-f^\prime\in Z_{\mathfrak{g}}(e)$, 但却拥有负特征根 w.r.t. h.

2. 对于 $(e,f,h)$ 和 $(e,f^\prime,h^\prime)$, 有 $h-h^\prime\in \ker(e)\cap \operatorname{im} (e)$. 于是 $h^\prime\in h+\mathfrak{u}$, 存在 $u\in U$, $h^\prime=uhu^{-1}$.

于是 3.7.3 证毕.

现在对于 $(e,f,h)$, 记 $G_{\mathfrak{sl}_2}$ 为 $(e,f,h)$ 的 simultaneous centralizers. 有

Prop 3.7.23: $G_{\mathfrak{sl}_2}$ is a maximal reductive subgp. of $Z_G(e)$ and $U$ is the unipotent radical of $Z_G(e)$.

首先, reductive 的 centralizer 是 reductive. 因此 $G_{\mathfrak{sl}_2}$ reductive. 其次, reductive gp 在 affine space 上的作用总有不动点. 于是对于 $R$ reductive, $R$ 在 $h+\mathfrak{u}$ 上的作用有不动点. 于是 by conjugation 我们不妨设 $R$ fix $h$. 那他当然也得 fix $f$. 因此他 fix $(e,f,h)$.

他在这里写了一个 basical 的方法说明 $Z_G(e)=G_{\mathfrak{sl}_2}\cdot U$. 不难, 跳了()

recall $\mathfrak{g}=\oplus \mathfrak{g}_i$

Lem 3.7.24: The subspace $\mathfrak{g}_2\subset \mathfrak{g}$ is stable under the adjoint $Z_G(h)$-action and the $Z_G(h)$-orbit of $e$ is Zar-open in $\mathfrak{g}$.

这是因为 $\operatorname{Lie}Z_G(h)=\mathfrak{g}_0$. 而 $[\mathfrak{g}_0,\mathfrak{g}_2]\subset \mathfrak{g}_2$, $[\mathfrak{g}_0,e]=\mathfrak{g}_2$. 然后根据代数群的知识即证.

本章的最后一步, 就是证明 3.7.1. Bourbaki 给出了一个比较 tricky 的证明. 而我们这个证明与之不同.

记 $\mathfrak{g}^e=Z_\mathfrak{g}(e)$.

Step 1: 对 $\dim \mathfrak{g}$ 归纳, reduce 到 $\mathfrak{g}^e$ 只包含 nilp element 的情况. 取 $x=s+n\in \mathfrak{g}^e$ abstract Jordan decopm. $s\neq 0$ s.s. 于是, $[s,e]=0$. $\tau=Z_\mathfrak{g}(s)$ proper reductive 且 $\dim \tau<\dim \mathfrak{g}$, 完成 reduction.

Step 2: 说明存在 $h$, $[h,e]=2e$. 实际上, 3.2.16 implies 了这个. 我们有 $(e,\mathfrak{g}^e)=0$, 有, $e\in \operatorname{im}(\operatorname{ad}e)=\ker(\operatorname{ad}e)$. 于是存在 $h$, $[2h,e]=2e$.

Step 3: 说明存在 $f$. 这实际上就是说 $h\in \operatorname{im}(\operatorname{ad}e)$, 也就是说 $(h,\mathfrak{g}^e)=0$. 也就是说

根据 Jacobi identity, 不难说明 $[h,\mathfrak{g}^e]\subset \mathfrak{g}^e$. 于是 $\mathbb{C}\cdot h+\mathfrak{g}^e$ 是一个 Lie subalg. 根据 Step 1, 不妨设 $\mathfrak{g}^e$ nilp. $\mathbb{C}\cdot h+\mathfrak{g}^e$ solvable. 于是 by Lie’s Thm, 我们可以将 $\mathfrak{g}$ 中元素同时上三角化 w.r.t. $\mathbb{C}\cdot h+\mathfrak{g}^e$. 而 $\mathfrak{g}^e$ 中元素 nilp. 主对角线元素自然全为 $0$, 得证.

下班!