Kac-Moody Pre 的准备
同样的, 也一样结束了()
好热
由于老师BV是外国人, 只能用英文了()
ok
We shall talk about the affine Lie algebra of nontwisted case. Take $\mathfrak{g}^\prime=\mathbb{C}[t,t^{-1}]\otimes_\mathbb{C}\overset{\circ}{\mathfrak{g}} +\mathbb{C} K$. Consider the “base” Lie algebra $\overset{\circ}{\mathfrak{g}}$ with nondegenerate invariant bilinear form $(\cdot|\cdot)$. Take ${u_i},{u^{i}}$ dual basis. We have Casimir operator
\[\overset{\circ}{\Omega}=\sum u_iu^i.\]We know that the Casimir operator is independent w.r.t. the choice of basis. Then, in particular,
\[\overset{\circ}{\Omega}=\sum u_iu^i=\sum u^iu_i\implies \sum_i [u_i,u^i]=0.\]And this proves that
\[\sum_i [u_i^{(m)},u^{i(n)}]=\sum_i [u_i,u^i]^{(m+n)}+m\delta_{m,-n}K=m\delta_{m,-n}(\dim \overset{\circ}{\mathfrak{g}})K.\]Now, recall that we have defined the generalized Casimir operator acts on reduced module
\[\Omega=2(K+\check{h})d+\overset{\circ}{\Omega}+2\sum_{n=1}^\infty \sum_i u_i^{(-n)}u^{i(n)}.\]of $\mathfrak{g}=\mathfrak{g}’+\mathbb{C} d, [d,x^{(n)}]=nx^{(n)}$.
We shall, for the $\overset{\circ}{\mathfrak{g}}=\overset{\circ}{\mathfrak{h}}\oplus(\oplus\mathbb{C} e_\alpha)$, since for $e_\alpha,e_{-\alpha}$ the chosen dual basis, $[e_\alpha,e_{-\alpha}]=\nu^{-1}(\alpha)$. Then
\[\overset{\circ}{\Omega}=\sum_{i} h_ih^i+2\nu^{-1}(\overset{\circ}{\rho})+2\sum_{\alpha\in \overset{\circ}{\Delta}_+}e_{-\alpha}e_{\alpha}.\]Now, we shall consider the restricted completion $U_c(\mathfrak{g}’)$ that is, $\sum_{j=1}^{\infty}u_j$ with $u_j\in U(\mathfrak{g}’)$ s.t. for all $v\in V$ reduced module, $u_j(v)\neq 0$ for all but finitely many $u_j$. Now, there are $d_n=-t^{n+1}\frac{d}{dt}$ extend to $U_c(\mathfrak{g}’)$.
Now, define the Sugawara Operators $T_n(n\in \mathbb{Z})$:
\[T_0=\sum_i u_iu^i+2\sum_{n=1}^{\infty}\sum_i u_i^{(-n)}u^{i(n)},\]\[T_n=\sum_{m\in \mathbb{Z}}\sum_i u_i^{(-m)}u^{i(m+n)},n\neq 0.\](need to explain, why $T_n\in U_{c}$.)
We have,
Lemma 12.8: a) For $x\in \circ\mathfrak{g}$, $m,n\in\mathbb{Z}$,
\[[x^{(m)},T_n]=2(K+\check{h})mx^{(m+n)}.\]b) $V$ restricted $\mathfrak{g}$-mod, $v\in V$ s.t. $\nn_+v=0,h(v)=\langle\lambda,h\rangle v$ for some $\lambda\in\mathfrak{h}^*$, then $T_0(v)=(\bar{\lambda}|\bar{\lambda}+2\bar{\rho})v$.
Proof: (a) We proof this in the semidirect product (to in duces $d_n$) $\mathfrak{d}\ltimes U_c(\mathfrak{g}’)$.
\[T_0=-2(K+\check{h})d+\Omega.\]Then,
\[[x^{(m)},T_0]=[x^{(m)},2(K+\check{h})d_0]=2(K+\check{h})mx^{(m)},\]for $[K+\check{h},x^{(m)}]=0$.
Secondly, we could check (on Pad) that
\[T_j=\frac{1}{j}[d_j,T_0],j\neq 0\]Then, (By one Jacobi identity on Pad)
\[[x^{(m)},T_j]=2(K+\check{h})mx^{(m+j)}.\]For (b), there are
\[\begin{align*} T_0(v)&=(\sum_i u_iu^i+2\sum_{n=1}^{\infty}\sum_i u_i^{(-n)}u^{i(n)})v\\ &=(\sum_i u_iu^i) v\\ &=(\sum h_ih^i+2\nu^{-1}(\rho))v\\ &=(\langle\lambda,h_i\rangle\langle\lambda,h^i\rangle+2(\lambda|\rho))v\\ &=finish. \end{align*}\]And then, we shall calculate the Lie brackets of Sugawara operators. There are
\[\begin{align*} [T_m,T_n]&=\sum_{j\in\mathbb{Z}}\sum_i[u_i^{(-j)}u^{i(m+j)},T_n]\\ &=\sum_{j\in\mathbb{Z}}\sum_iu_i^{(-j)}[u^{i(m+j)},T_n]+[u_i^{(-j)},T_n]u^{i(m+j)}\\ &=2(K+\check{h})\sum_{j\in \mathbb{Z}}\sum_i((m+j)u^{(-j)}u^{i(m+j+n)}-ju_i^{-j+n}u^{i(m+j)}). \end{align*}\]replace $j$ by $j+n$ we obtain:
\[[T_m,T_n]=2(K+\check{h})\sum_{j\in\mathbb{Z}}\sum_i(m-n)u_i^{(-j)}u^{i(m+n-j)}.\]Thus, for $m+n\neq 0,m,n\neq 0$, we have
\[[T_m,T_n]=2(K+\check{h})(m-n)T_{m+n}.\]Note that, for $m=0$ or $n=0$, $m+n\neq 0$, we can still assume $n=0$ an perform the same argument.
It left to argue that $m+n=0$. Here, we shall assume $m\neq 0$. Then
\[T_m=\sum_{j\geq 0}u_i^{(-j)}u^{i(j+m)}+\sum_{j> 0}u_i^{(-j+m)}u^{i(j)}.\]\[\begin{align*} [T_m,T_{-m}]&=\sum_i [u_iu^{i(m)},T_{-m}]+\sum_{j>0} \sum_i [u_i^{(-j)}u^{i(j+m)}+u_i^{(-j+m)}u^{i(j)},T_{-m}]\\ &=2(K+\check{h})m\overset{\circ}{\Omega}+2(K+\check{h}(j+m)u_i^{(-j)}-ju_i^{-j-m}u^{i(j+m)})\\ &\ \ +ju_i^{(-j+m)}u^{i(j-m)}+(m-j)u_i^{(-j)}u^{i(j)})\\ &=2(K+\check{h})(mT_0+\sum_{j>0}ju_i^{(-j+m)}u^{i(j-m)}-\sum_{j>0} ju_i^{-j-m}u^{i(j+m)}). \end{align*}\]And then, it equals to, by replace $j$ by $j+m$ in the first and $j$ by $j-m$, we obtain that (don’t want to copy kk)
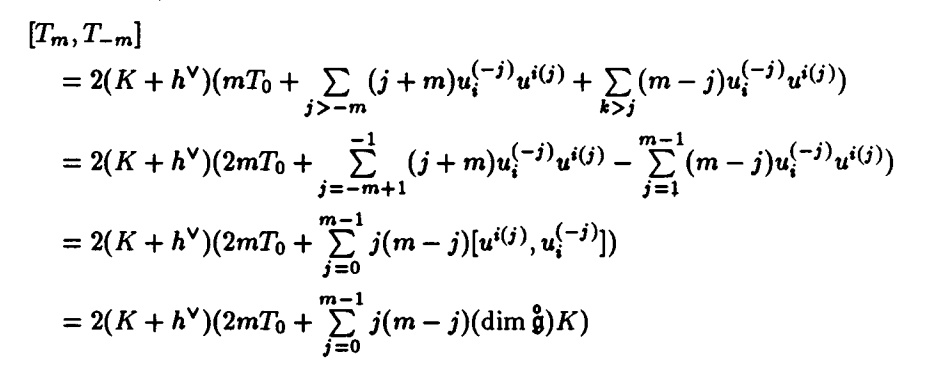
And there are $\sum_{j=0}^{m-1}j(m-j)=(m^3-m)/6$, there are
\[[T_m,T_n]=2(K+\check{h})((m-n)T_{m+n}+\delta_{m,-n}\frac{m^3-m}{6}(\dim\overset{\circ}{\mathfrak{g}})K).\]Now,(cor 12.8) by the above, for $V$ restricted $\mathfrak{g}’$-mod, $K$ scalar operator $kI$ with $k\neq \check{h}$, take
\[L_n=\frac{1}{2(k+\check{h})}T_n,n\in\mathbb{Z},\]\[c(k)=\frac{k(\dim\overset{\circ}{\mathfrak{g}})}{k+\check{h}},\]\[h_{\lambda}=\frac{(\Lambda+2\rho|\Lambda)}{2(k+\check{h})}, V=L(\Lambda).\]a) Letting
\[d_n\mapsto L_n,c\mapsto c(k)\]extends $V$ to a module over $\mathfrak{g}’+Vir$ ($\mathfrak{g}’\rtimes Vir$). In particular, $V$ extends to a module over $\mathfrak{g}=\mathfrak{g}’+\mathbb{C} d$ by $d\mapsto -L_0$.
b) If $V$ is the $\mathfrak{g}$-mod $L(\Lambda)$, $L_0=h_\Lambda I-d$.
$c(k)$: corformal anomaly of the $\mathfrak{g}’$-mod $V$,
$h_\Lambda:$ vacuum anomaly of $L(\Lambda)$.
For nontwisted affine algebra $\mathfrak{g}$ we have the “strange” formula of Freudenthal-de Vries:
\[\frac{|\bar{\rho}|^2}{2\check{h}}=\frac{\dim \overset{\circ}{\mathfrak{g}}}{24}.\]($\bar{\rho}=\rho-h^\vee\Lambda_0$, with $\Lambda_0$ the fundamental weight corresponds to $\alpha_0^\vee$, the simple imaginary root).
For the so-called modular anomaly,
\[m_{\Lambda}=\frac{|\Lambda+\rho|^2}{2(k+h^{\vee})}-\frac{|\rho|^2}{2h^\vee},\]\[m_\Lambda=h_\Lambda-\frac{1}{24}c(k).\]Prop 12.8: $V$ restricted $\mathfrak{g}’$-mod with a non-deg contravariant Hermitian form. Then the operator $T_n$ and $T_{-n}$ are adjoint w.r.t. the form.
recall $w_0:e_i\mapsto f_i,f_i\mapsto -e_i,h\mapsto -h$ for $h\in \mathfrak{h}_\mathbb{R}$ the compact involution, with $\mathfrak{l}(A)$ the fixed point set of $\mathfrak{g}(A)$.
There are $(\cdot|\cdot)$ is negative def. on $\overset{\circ}{\mathfrak{l}}$. Then we choose $v_i$ s.t. $(v_i|v_j)=-\delta_{ij}$, then for $u_i=\sqrt{-1}v_i$, there are $u_i=u^i$, $w_0(u_i)=-u_i$, thus $w_0(u_i(n))=-u_i(n)$ and thus the contravariant Hemitian form $H$ means that
\[H(g(x),y)=-H(x,w_0(g)y).\]Finishes the proof.
The last remark is for, $\circ{\mathfrak{g}}_\mathbb{R}$ f.d. v.s. over $\mathbb{R}$ with p.d. bilinear form $(\cdot|\cdot)$, $\overset{\circ}{\mathfrak{g}}$ complexification, $(\cdot|\cdot)$ extend by bilinearity. Take $h^\vee=0$ we have
\[c(k)=\dim \overset{\circ}{\mathfrak{g}},h_\Lambda=\frac{(\Lambda|\Lambda)}{2k}\]with $k=\langle\Lambda,K\rangle$ the level of $V$.
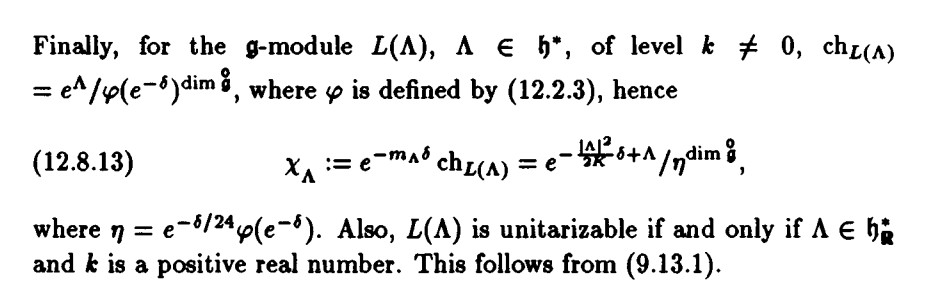
where $\delta|_{\mathfrak{h}+C}=0, \langle\delta,d\rangle=1, \phi(q)=\prod_{n=1}^{\infty}(1-q^{n})$, $\chi_\Lambda$ normalized character.
做这个 pre. 主要是下个学期要学共形场论了. 也许现在应该先打打基础()
这个 Sugawara operator 挺重要的.
